AI Insights: Understanding Bias and Variance: Why Models Fail

When Machine Learning models don’t perform well, the issue often comes down to two key factors: bias and variance. Understanding these concepts is crucial to building models that generalize well to new, unseen data. 🤖

What is Bias?:

Bias represents error due to overly simplistic assumptions in the model. A high-bias model pays little attention to training data and oversimplifies relationships, often leading to underfitting.

• Example: Using a straight line to model a highly complex dataset.
• Result: Poor accuracy on both training and test data.

What is Variance?:

Variance is the error due to model sensitivity to small fluctuations in the training data. A high-variance model fits the training data very closely (even noise), leading to overfitting.

• Example: A decision tree with too many branches capturing random patterns.
• Result: Excellent training accuracy but poor performance on new data.

The Bias-Variance Tradeoff:

An ideal model finds the right balance:

• Too much bias → underfitting.
• Too much variance → overfitting.

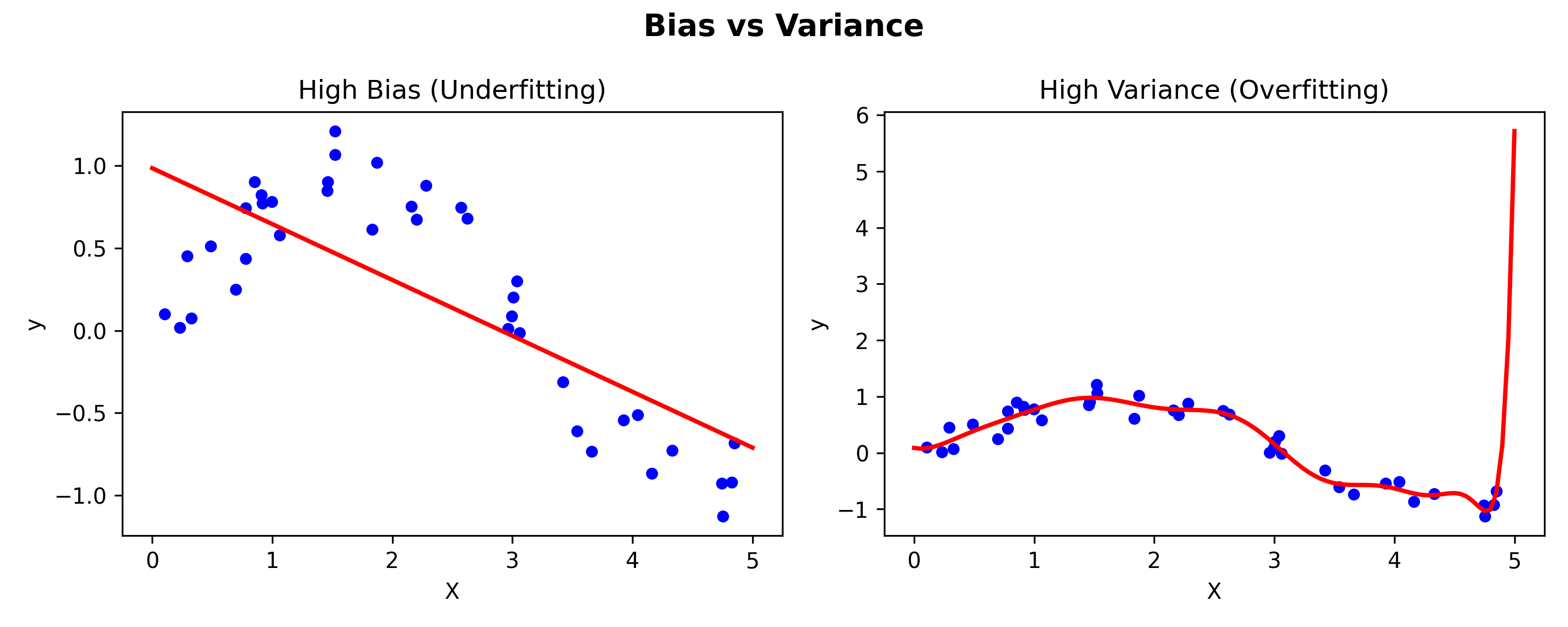
Figure: High Bias (Underfitting) vs High Variance (Overfitting)

Example Code (Scikit-learn):

Here’s how model complexity affects bias and variance using polynomial regression:

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import numpy as np

# Training data
X = np.array([1,2,3,4,5]).reshape(-1,1)
y = np.array([1,4,9,16,25])

# Simple model (high bias)
poly_low = PolynomialFeatures(degree=1)
X_low = poly_low.fit_transform(X)
model_low = LinearRegression().fit(X_low, y)
print("Low degree error:", mean_squared_error(y, model_low.predict(X_low)))

# Complex model (high variance)
poly_high = PolynomialFeatures(degree=10)
X_high = poly_high.fit_transform(X)
model_high = LinearRegression().fit(X_high, y)
print("High degree error:", mean_squared_error(y, model_high.predict(X_high)))

This shows how increasing model complexity can lead to higher variance even though training error decreases.

Conclusion:

Bias and variance are two sides of the same coin. Understanding and managing them is essential to prevent underfitting or overfitting, ultimately building models that perform well on real-world data. 🚀